Coupled Climate Dynamics

Tropical Pacific
Conceptual representation of coupled atmospere-ocean procesess in the tropical Pacific (Collins 2010)

Questions: How do atmospheric processes  interact with ocean processes to set the pattern of tropical warming on different time scales? How does this pattern feed back onto atmospheric clouds and circulation?
Theory: Atmospheric dynamics, cloud physics, physical oceanography; dynamical systems & control theory; stochastic models
Modeling: Global Climate Model simulations with idealized configurations and idealized forcing.
Observations: Satellite data and reanalysis.
Funding: NASA, DOE

 

Improved forecasts of future climate change

2 layer model
Probabilistic predictions of future warming from a model constrained to observations using a Bayesian approach

Questions: What recent observations best constrain future warming? What does a climate model’s skill in reproducing past changes tell us about its skill in forecasting future changes?
Machine Learning: developing and evaluating prediction schemes for optimal out-of-sample forecasts.
Methods: Theoretical models; analyzing output from Global Climate Models; perturbed physics ensembles; model-data fusion.
Funding: NOAA

 

 

Palaeoclimate

Laurentide
Ice Sheets over North America during the Last Glacial Maximum, some 21,000 years ago.

Questions: How were major climate processes such as radiative feedbacks & forcing different during past climate change events (e.g. Ice Ages). How can these processes be constrained from proxy information and how can they inform on future warming?
Theory & Modeling: Theoretical and numerical models for how climate responds to forcing across different temporal and spatial scales. General Circulation Models with idealized configurations.
Statistics & Data Science: Forward (stochastic) and inverse (bayesian) models linking physical process to measurable quantities (proxy records).
Funding: NSF

Climate Risk & Temperature Extremes

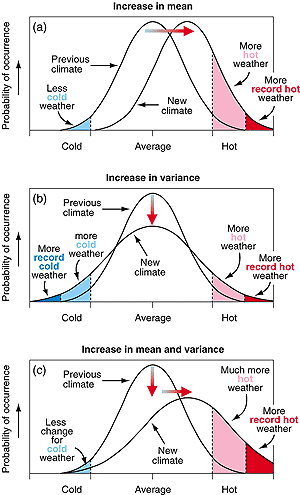
Working Group I: The Scientific Basis Get Javascript Other reports in this collection 2.7 Has Climate Variability, or have Climate Extremes, Changed? 2.7.1 Background Figure 2.32: Schematic showing the effect on extreme temperatures when (a) the mean ...
Examples of how temperature distributions may shift with climate change. (IPCC Assessment Report 4)

 

 

Questions: What determines the frequency of occurrence of regional temperature extremes heat waves?  What is the role of extremes in setting the cost of carbon?

Theory: Stochastic models of atmosphere-land coupling; Probabilistic forecast models of climate change; Integrated Assessment Models (Climate-Economics models).

Funding: University of Illinois Giess College of Business and School of Earth Society and Environment (SESE).